The word ``elastically" implies that both energy and momentum are conserved. Assume, the incoming photon is incident in the
 direction and scatters in the y direction. Then conservation of momentum gives: direction and scatters in the y direction. Then conservation of momentum gives: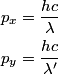 where 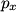 and and 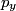 are the x and y components of the protons momentum after the collision, and are the x and y components of the protons momentum after the collision, and 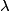 and and 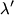 are the photons wavelengths before and after the collision, respectively. The initial energy is: are the photons wavelengths before and after the collision, respectively. The initial energy is: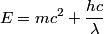 The final energy is 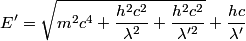 Equating the initial and final energy, we have that 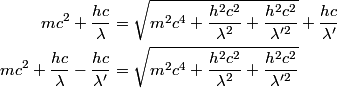 Square both sides and solve for 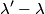 to find that to find that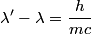 So, answer (D) is correct. |