(A) The amplitude is
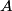 not not 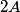 . . (B) The direction of the velocity can be found by required that the argument of the sine function is a constant: 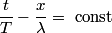 Increasing t a little bit requires you to increase x a little bit as well in order to maintain this equality, so the velocity in the positive x-direction. (C) The period is 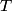 . . (D)  and and 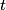 are variables here, so this cannot be right. are variables here, so this cannot be right. (E) Consider the equation above. Let 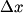 be the change in be the change in  during a small time interval during a small time interval 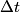 . Then, in order to maintain that equality we must have that . Then, in order to maintain that equality we must have that 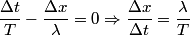 So, answer (E) is correct. |