We apply Gauss's Law in integral form:
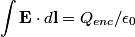 We take the closed surface to be a sphere of radius 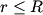 concentric with the sphere in the problem statement. Also, let concentric with the sphere in the problem statement. Also, let 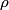 be the charge density, which we know is a constant. Then by Gauss's Law, we have, be the charge density, which we know is a constant. Then by Gauss's Law, we have, 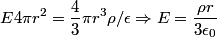 Thus, we see that the relationship between radius and electric field is a linear one, and so curve C must be correct. Hence the answer is (C). For 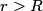 , the electric field falls off like , the electric field falls off like 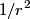 and is identical to the electric field produced by a point charge with charge and is identical to the electric field produced by a point charge with charge 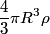 . . |