(A) This answer is correct.
(B) This statement implies that 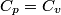 , which is well-known to be not true (and it clearly contradicts the problem statement). , which is well-known to be not true (and it clearly contradicts the problem statement).(C) This answer is not true, as one can easily show from the ideal gas law ( 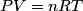 ). The temperature can remain constant while the pressure and the volume change. ). The temperature can remain constant while the pressure and the volume change.(D) This answer is somewhat ambiguous because of the words ``increase in the gas's internal energy." Assuming this means ``increase in the gas's internal energy as the temperature is increased by one degree Kelvin," then the statement is clearly incorrect. The increase in the gases internal energy per degree Kelvin is exactly the same for constant pressure processes and constant volume processes. The equation 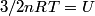 always holds for an ideal gas. (E) The words ``heat needed" here are somewhat ambiguous. ``Heat needed to do what?" is the obvious question If it means that ``heat needed to increase the temperature by one degree Kelvin," then this answer implies that 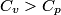 when in fact it is when in fact it is 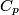 that is greater than that is greater than 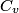 as it says in the problem statement. as it says in the problem statement. |